[ISL] 4장 - 분류(이론)

숫자형 변수를 예측했던 3장의 회귀문제와는 다르게, 질적 변수를 예측해야 하는 경우도 있다. 질적 변수(혹은 범주형 변수)를 예측하는 문제를 classification이라 부른다.

 

분류(classification)

 

분류방법들은 보통 각 범주에 속할 ‘확률’을 예측하는 형태로 분류를 한다.

예를 들면, 환자의 현재 상태를 체크한 데이터들을 보고 이 환자의 증상이 무엇인지를 분류하는 문제를 들 수 있다.

 

※ 위 문제를 회귀분석으로 접근할 수는 없을까? 

범주형 변수를 임의로(강제로) 숫자형 변수로 만들어주면 회귀분석이 가능은 하다.(예를 들어, 감기라면 Y=1, 폐렴이라면 Y=2, 독감이라면 Y=3 과 같은 식으로)

 

그러나 이는 잘못된 접근이다. 앞장에서도 다루었지만 임의로 숫자를 부여하게 되면, 감기와 폐렴의 차이(=1)가 폐렴과 독감의 차이(=1)와 같다는 의미가 되버린다. 또한, 변수가 2개일 때는 0과 1의 값으로 '마치 1이 나올 확률'로 시도는 가능하지만 [0,1]사이에만 존재하는 것이 아니라, 음수값이나 1.12 등도 나올 수 있기에, 확률값으로 볼 수가 없다.

 

따라서 범주형 자료를 예측하기 위해선, 분류의 목적에 맞게 고안된 다른 방법을 써야 한다.

 

1. 로지스틱 회귀 

로지스틱 회귀는 반응변수 Y가 ‘미납자가 될것인가 or 아닌가’와 같은 두 개의 범주를 나눌 때 주로 쓰인다.

특정 input에 대해 이 확률을 구한다면, 0.5이상일 경우 미납자로 치부해버리거나, 좀 더 위험을 피하고자 하는 회사라면 이 확률이 0.1 이상일 경우 미납자로 판단(임계치 조정)하는 등의 결정을 내릴 수 있을 것이다.

 

① 어떻게 모델링 할까?

앞서 이야기했듯이, p(X)=β0+β1X 식의 단순한 선형 적합으로는 ‘확률’의 의미를 띌 수 없다. 낮은 balance의 input에 대해선 음수를, 반대의 경우 1을 넘는 확률을 반환해 버리기 때문이다. 넘는 확률들을 0과 1로 치부해버려도, 특정 input에 대해 확률이 1, 즉 100%라는 현실적이지 않은 결과가 나오게 된다.

직관적으로 이해 할 수 있지만 binary classification(범주2개를 분류하는 문제)에서 선형 적합은 한계가 있을 수 밖에 없다.

 

위 문제를 boundary problem(음수와 양수의 끝이 없는 문제)이라 하는데 이를 해결하기 위한 여러가지 함수가 있지만 로지스틱회귀에선 로지스틱 함수라 불리는 다음 식을 쓴다.

로지스틱 함수

위 식을 이용하면 다음과 같이, 0과 1에 가까워지지만 절대 넘지는 않는 ‘확률’의 특성에 딱 맞아 떨어지는 함수형태가 만들어 진다.

왼쪽 그림 : 회귀분석, 오른쪽 그림 : 로지스틱 회귀분석

② 오즈(ODDS)의 등장

위의 식을 정리하면, 다음과 같은 식을 얻을 수 있다.

오즈(ODDS)

여기서 왼쪽 항은 ‘(해당클래스에 속할 확률)/(속하지 않을 확률)’을 의미한다. 이를 odds라고 부르는데, 0∼∞값을 가질 수 있고 각각 0일수록 매우 낮은 확률, ∞일수록 매우 큰 확률을 의미한다.

 

다음은 R을 사용하여 카드 부채(balance)와 미납자인지 아닌지에서 로지스틱을 적합한 결과이다.

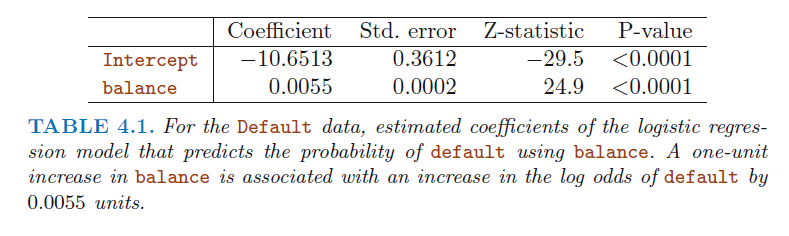
카드 부채의 계수가 0.0055이므로 balance가 1 증가할때 미납자에 대한 ‘오즈’가 e^0.0055배 증가한다고 해석 할 수 있다. 또한 이때의 p-value는 선형회귀에서 t분포를 사용한것과 다르게 z-분포를 사용하였고, 마찬가지로 standard error를 통해 추정의 정확도 역시 구할 수 있다.

 

③ 로짓(logit)의 등장

위 모형은 x에 대해 선형으로 값을 변경할 수 있으며 좌변에 log를 씌우는 형태이다. 식은 다음과 같다.

로짓(logit)

④ 최대우도추정법(Maximum likelihood)를 이용한 계수 추정

로지스틱 회귀에서는 반응변수는 범주형 변수이나 모형을 통해 예측된 값은 확률이므로 최소제곱법 등이 정당화되기 어려우므로 주로 최대우도추정법으로 추정한다.

 

최대우도추정법이란, 간단하게 관측값들을 토대로 결정을 내리는 방법이라 보면 된다. 실제 함수의 parameter θ를 추정할 때, 해당 관측값들을 토대로 θ가 취할 수 있는 여러 값 중 ‘그 관측값을 만들어 냈을 가능성이 가장 큰 값’을 θ로 추정하는 방법이다.

 

일차원적으로 예를 들면, 미납자class의 데이터는 1을 많이, 미납자가 아닌 class는 0을 많이 반환하는 모델을 만드는 것이다.

 

⑤ 다중 로지스틱 회귀와 confounding

책의 예제에서 단순히 미납자~학생(인지 아닌지)으로 적합하였을 때는 ‘학생이면 미납자일 확률이 더 크다’로 나왔었는데, 학생(X1)과 부채(X2)로 적합하였더니 ‘학생이면 미납자일 확률이 더 작다’를 의미하는 결과가 나왔다.(심지어 p-value가 둘다 유의하게 나왔는데도)

 

이는, 다중회귀에서의 계수가 다른 변수들이 ‘고정’된 상태에서의 의미, 즉 동일한 부채(balance)에서 학생들이 미납자일 확률이 작다를 의미하기 때문이다. 이는 그림을 통해 알 수 있다.

왼쪽 그림에서 빨간 곡선은 부채에 따른 학생의 미납자 비율, 파란색은 비학생이다.(아래의 빨간 직선, 파란직선은 전체의 미납자 비율)

 

같은 balance 수준(X) 내에서는 학생의 미납자 비율이 더 낮지만, 전체적으로 보았을때는 학생의 미납자 비율이 더 높다.

balance 정보가 없으면 전체로 보아 학생이 더 미납자가 될 확률이 크다고 판단할 수 있지만 balance 정보가 있을 경우 학생이 미납자가 될 확률이 더 작다라고 판단할 수 있게 되는 것이다. 

 

이렇게, 변수 자체에 correlated된 관계가 있을 경우 하나의 변수만을 이용하는 것은 다른 결과를 가져 올 수 있다. 이를 confounding문제 라고 부른다. 즉, 2개 이상의 범주에서의 로지스틱 회귀을 하는 것은 성능이 다른 모델에 비해 안좋다. 따라서, 실제에서 그렇게 자주 쓰이진 않으며 대표적인 대안 중 하나가 선형판별분석이다.

 

2. LDA(Linear Discriminant Analysis)

직접적으로 P(Y=k|X=x)를 구했던 로지스틱 회귀와는 조금 다르게, LDA에서는 조금 덜 직접적인 방법을 쓴다.

각각의 Y가 주어졌을때의 X의 분포, 즉 P(X|Y) 를 통하여 ‘Bayes theorem’으로 P(Y=k|X=x) 를 추정하고자 한다. 이 때 X의 분포 P(X|Y)에 정규 가정이 생긴다면, 로지스틱 회귀와 매우 유사한 형태가 된다.

 

※ 매우 유사한 형태가 된다면, 왜 굳이 로지스틱 회귀가 아닌 LDA를 사용할까?

• 2개 이상의 범주가 있을 시 성능이 더 뛰어나다
• 범주가 명확하게 구분되 있을 경우, 로지스틱 회귀는 굉장히 불안정한 결과를 내지만 LDA는 그렇지 않다. (범주가 명확하게 구분되어 있다는 것은 0 1의 분류에서 보통은 한 x 수준에서도 0인 data도 1인 data도 어느 정도 겹쳐있기 마련인데 0인 x의 수준과 1인 x의 수준이 극단적으로 나뉘어져 있는 경우를 말한다.)
• 자료의 개수 n이 적을때에도 각 클래스에 대한 X의 분포가 정규분포와 유사하다면, 역시나 로지스틱 회귀보다 안정적인 성능을 보인다.

① LDA for p = 1

P(X=x|Y=k)=fk(x) 를 추정하기 위해, 위에서도 언급하였듯이 분포를 가정한다. 가장 대표적으론 정규가정을 하는데, 수식으로 표현하자면 이렇다

즉, 각각의 평균과 분산 k=1,..,K인 K개의 각기 다른 정규분포가 있는 것이다. 추가로 모든 k에 대해 분산이 σ로 동일하다는 가정, 즉 등분산 가정을 한다. 이 경우 다음과 같은 수식으로 변화할 수 있다.

그 후 저 확률이 가장 큰 k클래스에게로 분류를 해주는 것이다. 또, 위의 확률 pk(x)에 log를 씌우고, 어떤 k에 대해서든 변하지 않는 중복된 term을 없애면 결국 다음 수식이 가장 큰 클래스k를 고르는 문제로 귀결된다.

이 경우 정규가정과 등분산 가정 하에서 공통분산σ^2와 각 클래스에 대한 parameter μk를 알고 있다면, 정확한 Bayes classifier를 계산으로 도출할 수 있다.

LDA는, 바로 이 공통분산σ^2와 각 클래스에 대한 parameter μk를 추정하여 Bayes classifier에 근사하고자 하는 것이다.

 

parameter는 다음과 같이 추정한다.

Linear Discriminant라는 명칭은 최종 function인 δhatk(x)가, 즉 최종 결정을 내리는 decision boundary가 xx에 대한 선형식으로 나오기 때문이다.

위 그림과 같이 초록과 빨강 각각 20개의 simulated 데이터가 있다면, 각 클래스(초록, 빨강)에 대해 πhatk, μk, σ를 추정하고 이를 통해 δhatk(x)가 큰 클래스로 분류를 하는 것이다.(즉, pk(x)=P(Y=k|X=x)의 추정확률이 제일 큰 클래스로 분류하는거랑 같은 말이다.)

 

해당 그림에서 실선은 decision boundary이다. simulated 데이터인 만큼 엄청난 데이터를 만들어 내어 구한 실제 boundary(Bayes classifier)가 점선으로 나와 있는데, simulated test data에 대하여 Bayes는 error rate가 10.6%, LDA는 error rate가 11.1%로 상당한 성능을 보였음을 알 수 있다.

 

최종 정리하자면, LDA는 fk(x)=P(X=x|Y=k)에 대한 정규 가정과 각 클래스마다 다른 평균, 동일한 분산 을 가정하여 Bayes classifier의 확률을 추정하는 방법이다.

 

② LDA for p > 1

변수가 여러개인 경우의 LDA에 대해 생각해보자. P(X=x|Y=k)=fk(x)엔 정규분포를 가정하였지만, 이젠 X=(X1,..,Xp)X=(X1,..,Xp)가 다변량 정규분포를 따른다고 가정한다. 즉, k 클래스에 속한 관측치들의 분포 P(X=(x1,..,xp)|Y=k)=fk(x)가 다변량 정규분포, 즉 N(μk,∑)를 따른다고 가정한다.

 

※ 다변량 정규분포란?

다변량 정규분포는 각각의 변수들이 1차원의(기존의 알고 있는) 정규분포 하나를 따르고 각각의 변수 pair가 어떠한 correlation를 가지고 관계를 갖는 분포이다. 쉽게 말해 다차원 정규분포라고 받아들이면 편하다.

 

이를 이용하여 다시 bayes 정리를 통해 Bayes classifier의 확률을 구하면 결국 다음의 식을 최대화하는 k클래스를 고르는 문제로 귀결된다. 이 경우 역시 결정에 관여하는 함수식 δk(x)가 x의 선형함수이기에, LDA라고 부른다. 

선형판별함수

예시로, 변수가 2개이고 클래스K가 총 3개일때 다음과 같이 결과가 나온다.

왼쪽 그림은 클래스 k가 k=1,2,3인 각 경우에 P(X=(x1,x2)|Y=k)=fk(x)를 추정하여 boundary를 그은 것이다. 저기서 각 원들은 각 분포의 95%신뢰 구간이다.

오른쪽 그림은 실제분포에서 20개씩 관측치를 뽑아 만든 LDA와 Bayes classifier를 비교해본 그림이다. error rate가 각각 0.0746, 0.0770으로 비슷한 수준의 성능을 보였다.

 

※ NULL Classifier의 발생

위와 같이 결과가 나오면 좋으나, 책의 예시를 보면 default(미납자)를 예측하는 모델을 만들고자 할때 좀 더 흥미로운 문제가 발생한다. 10000개의 training data에 대해 적합한 LDA는 2.75%의 낮은 오류율을 보였다. 그러나, 모델을 적합시킬때, 다음과 같은 점을 고려해야 한다.(즉, 오류율만으로는 측정할 수 없다는 것이다.)

 

• Traning data에만 지나치게 잘 적합되어 있는 것이 아닐까?(즉, Overfitting 문제가 발생된 것이 아닐까?

그러나 지금은 10000개의 data에 대해 2개의 parameter를 추정하고자 하였기에, 여기에선 overfitting 문제는 아니다.

 

• 전체 training data 중 default의 비율이 몇인가? 즉, 아무것도 하지 않은 null classifier에 비해 성능이 어느정도 좋은가?

실제로 training data 중 default(미납자)의 비율은 3.33% 밖에 되지 않았다. 즉, LDA의 train error 2.75%는 그 자체로 평가되어야 하는게 아니라, 위의 3.33%를 고려하여 평가해야 하는 것이다.

 

LDA가 default라고 평가한 104명중 81명이 실제 default라서 default라 평가한 사람들에 한해서는 잘한것 같다.

그러나, 전체 10000개의 data 중 non-default 9,667명 중에서는 9,664명을 non-default라고 옳게 평가하였지만, 실제 미납자 333명이 있는데, 그중 81명만을 default라고 제대로 평가하였다. 이는 무려 default인 사람 중 252/333=75.7%를 놓친 것이다.

 

이를 sensitivity와 specificity로 명명하는데, 민감도는 ‘목표 class를 제대로 잡아내었는지’, (여기선 81/333=24.3%) 특이도는 ‘반대 class는 제대로 잡아내었는지’, (여기선 9,644/9,667=99.8%)이다.

 

※ 이러한 low sensitivity가 발생되는 이유와 해결 방안

1. 원인

우리가 따라하려 목표로 한 Bayes Classifier가 ‘어떤 class를 틀리던간에 상관 없이’, 전체 ‘total error rate를 줄이고자’ 목표하였기 때문이다.

쉽게 말해 non-default라고 평가하면 ‘주로’ 맞으니까(train error가 적으니까), default라고 평가하는 것에 대해 매우 신중해진 것이다.

 

2. 해결방안

범주가 두 개인 경우 베이즈 분류기는 다음과 같은 조건을 만족하는 관측치에 한하여 default=YES로 분류한다.

민감도를 향상시키기 위해서 임계치를 0.5에서 0.2로 바꾼다면 즉, default일 확률이 0.2정도만 되어도 default로 평가하는 것이다.

다음은 임계치를 0.5에서 0.2로 바꾸었을 때 결과이다.

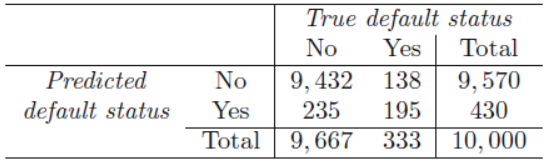
이제 민감도의 관점에서, 전체 333명 중 138명, 즉 41.4%를 놓치게 되어 75.7%였던 지난 모델보다 훨씬 나은 결과를 보여주었다. non-default를 그만큼 더 못 판별하여 전체 total error-rate는 3.73%으로 늘어나게 되었지만 default를 잘 잡아내고자 하는 credit-card회사의 관점에서는 민감도가 낮은 이 모델이 더욱 좋은 모델인 것이다.

 

※ 비교를 위한 ROC curve

여러 threshold의 오류율을 비교하고자 할때,  ROC curve가 주로 이용된다. 민감도와 특이도를 동시에 나타내어 분류기의 성능을 평가하는 대표적인 시각화 방법이다. 

 

ROC curve는 임계치를 변화시키면서 (1-특이도,민감도)를 2차원 좌표평면 상에 나타낸 곡선으로써, 이상적으로는 왼쪽 상단을 통과하는 것이 좋고, 이 경우 곡선 아래 면적이 1이 된다. 여기서 곡선 아래 면적을 AUC(Area Under Curve)라 한다.

ROC Curve

3. QDA(Quadratic Discriminant Analysis)

QDA는 P(X=(x1,..,xp)|Y=k)=fk(x) 에 대하여 multivariate normal 분포를 가정하여 Bayes’ theorem을 이용한 분류를 한다는 점에서는 똑같지만, 모든 클래스k에 대하여 동일한 covariance matrix를 가정했던 LDA와 달리 QDA는 k클래스 마다 각각의 covariance matrix를 가지게 한다. 즉, X∼N(μk,∑k)를 갖게 하는 것이다. 식으로 나타내면 다음과 같다.

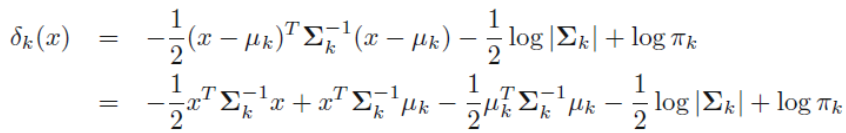
QDA의 판별함수

 

※ 분산이 동일하다 가정하는 LDA vs 분산이 다르다 가정하는 QDA

왜 굳이, 분산이 동일하다 가정하는 LDA와 다르다 가정하는 QDA로 두 개의 방법이 있을까?

답은 간단하게 bias-variance trade-off에 있다. p개의 예측변수가 있다면 그들의 covariance matrix를 추정하기 위해선 p(p+1)/2개의 parameter가 필요하다. k개의 클래스에 대해 다른 분산으로 추정하려면 K*p(p+1)/2개의 parameter를 추정해야 하는 것이다. 

 

작은 수의 parameter를 추정하는 LDA의 경우는 훨씬 덜 flexible하고 variance가 적은 모델이 된다. 그러나, 기본 가정인 공통분산이 아닐 경우, 높은 bias를 갖게 될 것이다.

 

즉, 정리하면 LDA와 QDA를 사용하는 상황은 다음과 같다. 

• Traning Data 수가 적어서 Variance를 줄이는 것이 중요할 경우 LDA를 사용

• Data 수가 많아서 Variance에 대한 우려가 적을 때, 혹은 공분산에 대한 가정이 비현실적으로 판단될 때에는 QDA를 사용한다.

4. KNN(K-nearest neighbors)

KNN은 가장 가까운 k개의 관측치를 보고 그들의 특성에 따라 분류를 하는 것으로, 비모수적 방법이라고 볼 수 있다.

조건부 확률을 인접한 K개의 Data Points의 상대비율로 추정하며 다음과 같이 나타낼 수 있다.

여기서, N0는 x0와 가장 가까운 K개의 자료의 집합을 나타낸다. 위 확률을 최대로 하는 j로 관측치를 분류하며, k의 선택이 분류기의 성능을 결정하는데 매우 핵심적인 역할을 한다.

 

예를 들면 아래의 그림과 같이 3개의 범주, k=7일 때,

KNN 예제

초록색 점을 기준으로 7개의 Data를 하나의 집합으로 만든 후, 확률을 다음과 같이 구할 수 있다.

 

• P(Y=x | x=0) = 3/7
• P(Y=x | x=0) = 2/7
• P(Y=x | x=0) = 2/7

※ K의 역할

위의 예를 보면 알 수 있듯 K의 역할은 굉장히 중요하다. K를 너무 크게 잡으면 집합의 크기가 넓어져서 비정확하며, 작게 잡으면 Data가 너무 적은 상황이 만들어진다. 또한 K=1일 경우에는 Perfect Fit이 일어나게 되므로 좋지 않다.

 

5. 분류 방법들의 비교

1. LDA vs. 로지스틱

LDA와 로지스틱 회귀는 접근 방식은 달랐지만 굉장히 유사한 밀접한 관계를 갖는다. 1개의 예측변수에 대해 2-클래스로 분류하는 문제를 보았을때, LDA로 로짓(log odds)를 계산해 보면 다음과 같다.

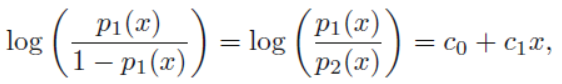
로지스틱에서 로짓이 다음 식으로 x에 대한 1차식으로 나타내어지는 것과 같다.

물론 로지스틱은 계수를 maximum likelihood로, LDA는 정규가정하에서 mean 과 variance의 추정으로 계수를 구하였기에(차이점) 이 둘의 계수 자체가 일치하지는 않지만, 선형 decision boundary를 만들어 낸다(공통점). 성능은  LDA의 가정(정규가정)이 어느정도 맞을 경우 LDA가 좋고, 틀릴 경우 로지스틱회귀가 좋게 된다

 

2. QDA vs KNN & LDA

QDA는 KNN과 LDA, 로지스틱회귀를 합친 특성을 가지고 있다. 

KNN보다는 flexible하지 않지만 decision boundary에 non-linear가정을 하였기에 LDA보다 flexible하고, 분포를 가정하였기에 KNN과 다르게 비교적 적은 데이터에서도 잘 적합할 수 있다.(LDA에 비해선 parameter수가 더 많으니 많이 필요하다.)

 

3. 실험을 통한 성능 비교

6개의 유형에 대한 시나리오 데이터를 통해 비교해보았다. 이때, 예측변수는 2개이며, K=2이다. 

• S1 : 각 범주내의 변수들은 서로 독립인 정규분포.
• S2 : 각 범주내 변수들의 상관계수가 -0.5. 다른 조건은 S1과 동일.
• S3 : 각 범주내의 변수들은 t분포. 
• S4 : 각 범주내의 변수들은 각각 상관계수가 0.5, -0.5인 정규분포. 
• S5 : 각 범주내의 변수들은 서로 독립인 정규분포. 반응변수가 두 변수의 이차결합으로 생성됨. 
• S6 : 각 범주내의 변수들은 서로 독립인 정규분포. 반응변수가 두 변수의 복잡한 비선형결합으로 생성됨.

분류기 종류는 다음과 같다.

• KNN, K = 1
• KNN, K는 교차타당검증법에 의해 결정
• LDA
• 로지스틱 모형
• QDA

1~3번의 시나리오를 비교했을 때는 다음과 같다.

시나리오1~3의 분류기 비교

- 시나리오 1. 1) LDA : LDA의 가정사항이 normal이므로 LDA가 가장 우수했다.  2) KNN & QDA : 지나친 flexible을 가졌기에 bias측면에서의 강점은 별로 부각되지 않으며, Variance가 커졌기에 우수하지 못했다 3) 로지스틱 : boundary가 선형이라는 점에서 LDA보다 약간 우수하지 못했다.   - 시나리오 2. : 시나리오 1가 동일하다.   - 시나리오 3. : LDA의 가정이 무너졌기에 로지스틱보다 조금 못했다.

4~6번의 시나리오를 비교했을 때는 다음과 같다.

시나리오4~6의 분류기 비교

- 시나리오 6. : 정규분포의 가정을 만족하고 있으므로 QDA가 가장 우수한 모습을 보인다. - 시나리오 5. : 이차 decision boundary. 즉, DT를 쿼드라틱으로 하겠다는 의미이다. 이는 많은 parameter들을 수용하고 있기에 QDA가 가장 우수한 모습을 보인다. - 시나리오 6. : 이 때는 DT의 제한이 없으므로 KNN-CV가 가장 우수한 모습을 보인다.

따라서, 모든 상황에서 우월한 분류기는 없음을 알 수 있다.

비교적 간단한 상황에서는 LDA or 로지스틱이 우수하다.

반대인 복잡한 상황(분포가 정규 분포가 아니고, DT가 복합한 경우)에서는 KNN or QDA가 우수하다.

KNN 또한 적절한 K를 설정하는 것이 중요함도 알 수 있다.

 

다음은 실제 "The Stock Market Data"를 통해 위 모형들을 적합하여 결과를 비교해 볼 것이다.