[ISL] 5장 - Resampling Methods(CV)

재표본(Resampling)

재표본(Resampling)은 통계학에서 빼놓을 수 없는 요소이다.

간단히 말하자면 이는 training set에서 반복해서 sample을 뽑고, 거기에 반복해서 model을 적합시켜보는 것이다. 이는 기존의 training set 전체를 단지 한번만 쓰는것 보다 더 추가적인 정보를 줄 수 있다.

 

여기에선 가장 많이 쓰이는 resampling method인 Cross-validation과 bootstrap을 다룰 것이다.

* 교재에서는 CV와 붓스트랩 모두 다루지만, 이 게시글에선 CV만 다루겠다.(정보가 필요하신 분은 Data Science 카테고리로 가시면 예제와 함께 있습니다.)

 

※ CV(Cross-Validation) 이란?

test error 와 training error는 다르다. 모델을 적합시키는데 쓰이지 않은, 즉 주어지지 않은 test set에 대한 오류율이 test error인데, 이걸 낮추는게 모델의 최종목적이라 할 수 있다. 반면 training error는 주어진 데이터에 대한 오류율로, 특히나 overfitting의 경우 실제 error율을 과소평가할 수도 있다.

 

평가를 하기 위한 test set이 따로 주어져 있다면 좋겠지만, 현실에선 그렇지 않은 경우가 훨씬 많다. 이를 해결하기 위해 2가지 방법이 쓰인다.

 

1) training error rate에 수학적인 보정을 가하여 test error를 간접적으로 추정하는것(6장에서 다룰 예정)

2) training set중 몇개를 따로 빼내서(hold out) test error를 직접적으로 추정하는 방법

 

여기서 2)가 CV에 해당하는 내용이다.

1. The Vaildation set Approach

Validation set approach는 test error을 추정하는 가장 간단한 방법인데, 간단하게 우리의 training data를 random하게 반 잘라서, test error 추정을 위해 따로 빼놓는 것이다.

 

그림으로 표현하면 다음과 같다.

The Vaildation set Approach 예시

training set에서 떨어져 나온 이 data set들을 validation set이라고 부른다. 남은 training set에서 적합을 시키고 이를 validation set에 대해 error rate를 구하여 test error rate를 추정하는 것이다.

 

※ 단점

이 방법은 랜덤하게 ‘반이나’ 자른다는 점이 이 방법의 장점(간단하다는 점에 있어)이자 단점이다. data set이 어떻게 잘리느냐에 따라서 model의 변동이 심하고, 그에 따라 test MSE의 추정치도 심하게 변화하기 때문이다. 여러 방법에 따른 test MSE를 추정하고자 하였던 원 목적을 생각해보았을때 이는 좋은 결과가 아니다.

 

즉, 정리하면 랜덤하게 분할하기에

 

1) 분할 결과에 따라 추정의 변동성이 클 수 있다.

2) 자료의 크기가 작거나 이상치가 포함되어 있다면 더욱 변동성이 커진다.

3) 원 자료의 크기보다 작은 집합의 훈련자료가 모형적합에 사용되므로 test error가 과대추정 될 수 있다.

 

이러한 결과를 얻을 수 있다는 것이다.

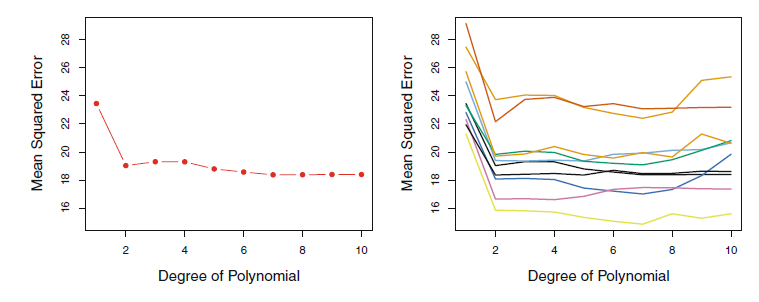
왼쪽은 validation set approach를 한번만 해본 것, 오른쪽은 10번 반으로 잘라서, 10번 해본 것이다. 둘 다 2차항 이상으로 적합하는 것에 큰 효과가 없음을 알려주긴 한다.

 

그러나 오른쪽 그림을 보면 다음과 같은 내용을 알 수 있다.

 

1) 어떻게 반으로 잘렸는지에 따라 추정된 test MSE의 변동이 천차만별이다.

2) 최적의 Vaildation MSE를 위한 차수도 천차만별이다.(즉, 어떤 차수를 쓸 것인지 불분명해진다.)

3) 자료의 수를 반으로 줄였다는 점에서 추정의 성능이 떨어지게 된다.(반만 적합한 모델은 덜 정확할 것이므로 전체 자료로 적합하였을 경우 모델이 가졌을 test MSE보다 더 클 수 밖에 없다.)

 

2. LOOCV(Leave One Out Cross Validation)

LOOCV는 validation set approach의 단점을 줄이고자 하는 방법이다.

 

이 방법은 validation set으로 반을 잘라내는 것이 아니라, 한개만 따로 빼낸다.

그리고 전체 자료n개중 나머지 n-1개의 training set으로 적합을 한뒤, 하나의 자료에 대해서 error rate를 계산한다.

그리고, 위의 방법을 모든 자료에 반복한다.

 

즉, 모든 자료n을 각각 한 번씩 빼고, 각각에 경우 남은 n-1개의 training set 에대해 전부 적합을 한다. 이 경우 각 추정된 n개의 test MSE가 생길 것이고, 이를 최종적으로 평균 내주어, test error를 추정한다. Test MSE에 대한 LOOCV 추정치는 다음과 같다,

 

LOOCV를 그림으로 표현하면 다음과 같다.

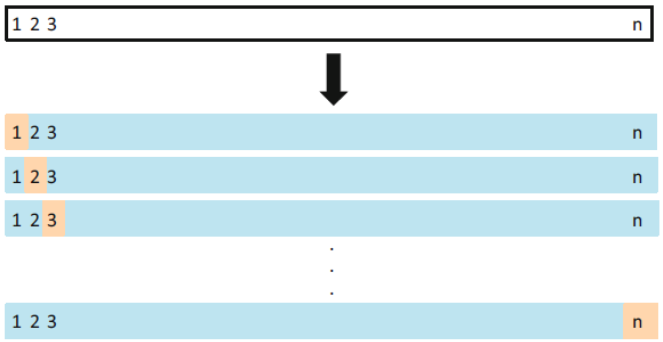
LOOCV의 예시

※ 장점

1) 데이터의 반만을 가지고 적합을 하는 validation set approach와 달리, n-1개를 가지고 적합을 하기에 전체 training data의 test MSE에 대해 할 수 있는 거의 가장 정확한 추정을 할 수 있다. 즉, bias가 매우 적다. 

2) 어떻게 training/validation을 나누느냐에 따라 결과가 달라졌던 validation set approach에 비해, LOOCV는 n번의 모든 경우를 자르고 평균을 내기에, 결과가 달라지지 않는다.

 

※ 단점

단점은 계산량이 매우 많아 자료의 크기가 매우 크거나 적합모형의 계산에 시간이 많이 소요되는 경우 적용에 제한이 따른다는 점이다.

 

위의 단점을 해결하고자하는 CV test error의 단순화에 대한 연구는 계속 진행중이다. 예를 들면, 다항회귀모형의 경우 다음과 같은 단순화가 가능하다.

여기서 hi는 hat matrix의 i번째 대각원소이며, 위 식을 사용할 경우 한 번의 모형적합을 통해 CV test error를 얻을 수 있다.

 

3. K-fold Cross-Validation

너무 단순한 validation set approach와 너무 손이 많이 가는 LOOCV. 그들의 중간점이 바로 이 k-fold CV(Cross-Validation)이다. 

 

먼저, K-fold CV를 그림으로 표현하면 다음과 같다.

전체 데이터를 특정한 수 k개의 그룹으로 random하게 나눈다.

그리고 첫번째 그룹을 빼고, 남은 k-1개의 그룹으로 모델을 적합시키는 것이다.

LOOCV에서 처럼, 이를 k번 반복한다.

최종적으로 나온 k개의 MSE를 평균을 내어 test MSE를 추정하며, 식은 다음과 같다.

식을 보면 알겠지만, k=n이 되면 LOOCV이며, 주로 k는 5 or 10으로 많이 적합한다.

 

※ 장점

1) K-fold CV는 LOOCV에 비해 계산량이 현저히 감소한다.

2) LOOCV에 비해 test error의 추정이 오히려 정확한 경우가 종종 발생한다.

 

※ 단점

k개의 집합으로 분할 시, 불확실성이 발생하여 test error 추정시 변동성이 발생한다는 점이 단점이다. 하짐나 이는 Vaildation set Approach보다는 훨씬 안정적이다.

 

4. LOOCV vs. K-fold CV

LOOCV와 K-fold를 분할변동성 측면에서 비교하면 다음과 같다.

K-Fold	LOOCV
분할변동성이 존재하면 1. 영향이 크지 않고 2. 계산량이 적으며 3. 상관성이 적다.	분할변동성이 존재하면 1. 영향이 있으며 2. 계산량이 많아지고

 

다음 그림은 LOOCV와 10-fold CV를 비교한 것이다.

성능에서는 큰 차이를 보이진 않으며, 10-fold CV의 결과를 보면 변동성이 적은 것도 알 수 있다.

파란선 : true test MSE, 주황선 : 10-fold CV로 구한 test MSE, 검은선 : LOOCV로 구한 test MSE

10-fold CV와 LOOCV로 구한 test MSE 모두 min이 되는 시점은 비슷하며, 둘 다 비슷하게 선을 그리고 있다.

그렇기에 2, 3번째 같은 경우에서는 계산량이 많은 LOOCV를 피하는 것이 좋을 수 있다.