[ISL] 4장 - 분류(R 실습)

* 이론 : https://kuklife.tistory.com/100?category=853435

* 소스코드 원본 : http://faculty.marshall.usc.edu/gareth-james/ISL

 

1. 기초통계량 확인

1. ISLR Package를 다운받은 후, Smarket을 load한다.

# Chapter 4 Lab: Logistic Regression, LDA, QDA, and KNN # The Stock Market Data install.packages("ISLR") library(ISLR) names(Smarket) dim(Smarket)

 

2. Summary()값을 확인하면 다음과 같은 결과를 얻을 수 있다.

summary(Smarket)

Direction을 보면 Up 혹은 Down으로 나뉘는데 무엇이 1인지 명확히 알 필요성이 있어보인다.

 

 

3. 각 변수들의 상관계수를 시각화 시켜본다.

pairs(Smarket)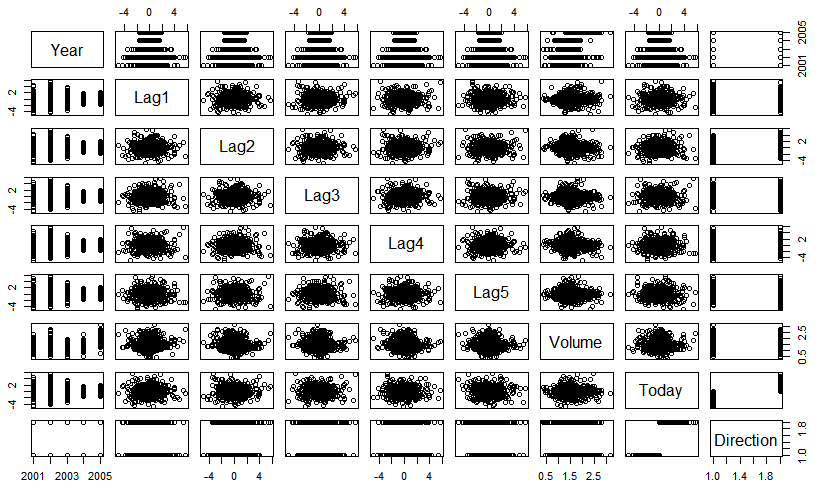

 

4. 불필요한 변수인 Direction을 제외한 8개의 상관계수를 구해본다.

cor(Smarket[,-9]) #9번째를 뺀 나머지의 상관계수

3, 4를 확인한 결과 상관계수가 높은 변수를 찾을 순 없었다.

 

2. LogitsticLogistic Regression

1. Direction에 Lag1,..,5와 Volume이 어떠한 영향을 미치는지 로지스틱 모형을 적합시켜 알아보자.

glm.fit=glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,data=Smarket,family=binomial) summary(glm.fit)

위의 결과를 보면 3가지를 알 수 있다.

 

1) Lag1과 Lag2은 부정적이므로 떨어지는 상황
2) Lag2~Lag5는 올라가는 상황
3) p-value를 보면 0.05보다 작아야하는데 작은 것이 하나도 없다.

 

 

2. 주어진 x에 대해 predict 확률을 구해본 후, 앞의 10개를 출력하면 다음과 같다.

glm.probs=predict(glm.fit,type="response")#type이 없으면 linear predictor, response이면 주어진 x에서 predict 확률 glm.probs[1:10]

0.5를 임계치로 잡으니 1, 4, 5, 6, 8, 9는 올라갈 것이라 보는 것이다.

 

 

3. 앞서 확인하였던 Up or Down으로 나뉜 Direction 변수를 어떤 것이 1인지 알아낸다.

contrasts(Direction)

 

4. 1250개의 모든 관측치들 중 glm.probs가 임계치에 해당하는 0.5 이상이 되면 up으로 바꾼다.

glm.pred=rep("Down",1250) #1250개의 관측치를 다 down으로 채움 glm.pred[glm.probs>.5]="Up" #예측확률이 0.5가 넘는 애들은 up으로 변경 table(glm.pred,Direction) #glm.pred 는 y het, Direction은 실제값인 y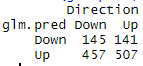

 

5. 위의 결과를 기반으로 확률값을 계산하면(507+145)/1250 = 0.5216 이 된다. 즉, true인 관측치에 대한 확률이다.

 

6. train data set과 test data set을 나눠야하므로, 2001~2004년의 data는 train, 2005년의 data는 test로 나눈다.

train=(Year<2005) #2001년부터 2004년의 자료를 train data-set으로 설정  Smarket.2005=Smarket[!train,] #시계열 데이터에선 과거를 train, 최신자료를 test(즉, 2004년까지는 train, 2005년은 test)  dim(Smarket.2005) Direction.2005=Direction[!train] #train이 아닌 관측치를 test set으로

 

7. train data set을 모형에 적합 후, 오분류율을 확인하면 다음과 같다.

glm.fit=glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,data=Smarket,family=binomial,subset=train) #subset=train을 하면 true인 애들만 적용하겠다 라는 의미 glm.probs=predict(glm.fit,Smarket.2005,type="response") #test set에서의 y를 예측(Smarket.2005는 test-set) glm.pred=rep("Down",252) #252개의 관측치 glm.pred[glm.probs>.5]="Up" table(glm.pred,Direction.2005) mean(glm.pred==Direction.2005) #test-set의 정분류율 48%(즉, 쓸모없는 모델...) mean(glm.pred!=Direction.2005) #test-set의 오분류율 52%

모형을 적합해본 결과 좋지 못한 결과를 얻게 되었다.

따라서, p-value가 작은 lag1과 lag2를 이용해서 모형 적합하면 향상된 결과가 나오지 않을까라는 생각으로 모델을 적합해본다.

 

 

8. p값이 낮았던 lag1과 lag2만 이용한 후 다시 모델 적합하면 다음과 같다.

glm.fit=glm(Direction~Lag1+Lag2,data=Smarket,family=binomial,subset=train)  glm.probs=predict(glm.fit,Smarket.2005,type="response") glm.pred=rep("Down",252) glm.pred[glm.probs>.5]="Up" table(glm.pred,Direction.2005) mean(glm.pred==Direction.2005)

쓸모없는 변수를 뺀 결과 56%가 되었다. 즉, 상승되었음을 의미한다.

 

3. LDA

1. LDA 또한 P-value가 낮았던 lag1과 lag2만 이용하여 모델에 적합하여 보자.

#install.packages("MASS") library(MASS) lda.fit=lda(Direction~Lag1+Lag2,data=Smarket,subset=train) lda.fit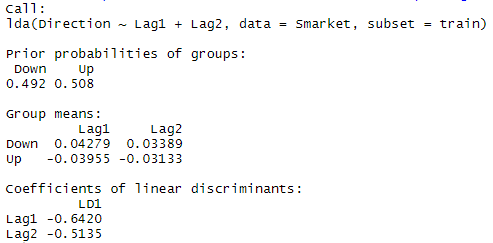

LDA는 up과 down의 비율 확인 가능하며, 두 그룹의 평균이 up은 nagative로 down은 positive쪽에 치우침을 알 수 있다.

 

 

2. test data set을 적합시켜보면 다음과 같다.

lda.pred=predict(lda.fit, Smarket.2005) lda.class=lda.pred$class table(lda.class,Direction.2005)

 

3. 따라서, 확률값을 계산해보면 다음과 같다.

mean(lda.class==Direction.2005)

확률값은 56%로써, 로지스틱 모형과 크게 차이가 없음을 알 수 있다.

 

4. QDA

1. QDA 또한 P-value가 낮았던 lag1과 lag2만 이용하여 모델에 적합하여 보자.

qda.fit=qda(Direction~Lag1+Lag2,data=Smarket,subset=train) qda.fit #group means가 약간달라짐을 확인가능 qda.class=predict(qda.fit,Smarket.2005)$class table(qda.class,Direction.2005) mean(qda.class==Direction.2005)

확률값은 60%로써, 앞서 보여줬던 2개의 모형보다 우수한 모습을 보인다.

 

5. KNN

1. 위와 동일하게 lag1과 lag2에 대해서만 data set을 나눈 후, k는 3으로 잡아보겠다. (같은 결과값을 위해 seed값을 고정하겠음)

library(class) train.X=cbind(Lag1,Lag2)[train,] test.X=cbind(Lag1,Lag2)[!train,] train.Direction=Direction[train] set.seed(1) knn.pred=knn(train.X,test.X,train.Direction,k=3) #1번째 인수에 훈련자료, 2번째 자료에는 테스트자료, 세번째 자료에는 훈련자료에서의 response y값, 4번째 인수에는 k값 table(knn.pred,Direction.2005) mean(knn.pred==Direction.2005)

확률값은 53%이다.

 

6. 평가

Smarket Data의 모형 적합 결과는 다음과 같은 순서로 분류율이 뛰어난 모습을 보인다.

 

1. QDA : 60%

2. 로지스틱 : 56%

3. LDA : 56%

4. KNN : 53%

 

※ 소스코드 전체

# http://faculty.marshall.usc.edu/gareth-james/ISL/
 
# Chapter 4 Lab: Logistic Regression, LDA, QDA, and KNN
# The Stock Market Data
# install.packages("ISLR")
library(ISLR)
names(Smarket)
dim(Smarket)
 
summary(Smarket)
 
pairs(Smarket)
 
#cor(Smarket)
cor(Smarket[,-9]) #9번째를 뺀 나머지의 상관계수
 
attach(Smarket)
plot(Volume)
 
# Logistic Regression 여기가 중요!!!
# 3일전~5일전의 거래량과 return들의 예측값 확인
# 출력결과 해석
# up 혹은 down인데 뭐가 1이냐를 알아야함
# 위의 답은 contrasts(Direction)결과를 통해 확인 가능
# Lag1과 Lag2은 부정적이므로 떨어지는 상황
# Lag2~Lag5는 올라가는 상황
# p-value를 보면 0.05보다 작아야하는데 작은 것이 하나도 없다.
glm.fit=glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,data=Smarket,family=binomial)
summary(glm.fit)
 
coef(glm.fit)
 
summary(glm.fit)$coef
 
summary(glm.fit)$coef[,4]
 
glm.probs=predict(glm.fit,type="response") #type이 없으면 linear predictor, response이면 주어진 x에서 predict 확률
glm.probs[1:10] #0.5를 임계치로 잡으니 1,4,5,6,8,9는 올라갈 것이라 보는 것
 
contrasts(Direction)
glm.pred=rep("Down",1250) #1250개의 관측치를 다 down으로 채움
glm.pred[glm.probs>.5]="Up" #예측확률이 0.5가 넘는 애들은 up으로 변경
table(glm.pred,Direction) #glm.pred 는 y het, Direction은 실제값인 y
 
(507+145)/1250 
 
mean(glm.pred==Direction) #true인 관측치에 대한 비교율
 
train=(Year<2005) #2001년부터 2004년의 자료를 train data-set으로 설정
Smarket.2005=Smarket[!train,] #시계열 데이터에선 과거를 train, 최신자료를 test(즉, 2004년까지는 train, 2005년은 test)
dim(Smarket.2005)
Direction.2005=Direction[!train] #train이 아닌 관측치를 test set으로
 
glm.fit=glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,data=Smarket,family=binomial,subset=train)#subset=train을 하면 true인 애들만 적용하겠다 라는 의미
glm.probs=predict(glm.fit,Smarket.2005,type="response") #test set에서의 y를 예측(Smarket.2005는 test-set)
glm.pred=rep("Down",252)
glm.pred[glm.probs>.5]="Up"
table(glm.pred,Direction.2005)
mean(glm.pred==Direction.2005) #test-set의 정분류율 48%(즉, 쓸모없는 모델...)
mean(glm.pred!=Direction.2005) #test-set의 오분류율 52%
 
glm.fit=glm(Direction~Lag1+Lag2,data=Smarket,family=binomial,subset=train) 
glm.probs=predict(glm.fit,Smarket.2005,type="response")
glm.pred=rep("Down",252)
glm.pred[glm.probs>.5]="Up"
table(glm.pred,Direction.2005)
 
mean(glm.pred==Direction.2005) #쓸모없는 변수를 뺐더니 56%(상승을 의미)가 됨(-> 유의미한 변수를 선택해주는 것도 하나의 방법이다)
 
(106+76)/252
 
predict(glm.fit,newdata=data.frame(Lag1=c(1.2,1.5),Lag2=c(1.1,-0.8)),type="response")
 
################################################
 
#install.packages("MASS")
library(MASS)
lda.fit=lda(Direction~Lag1+Lag2,data=Smarket,subset=train)
lda.fit #up과 down의 비율 확인가능, 두 그룹의 평균이 up은 nagative로 down은 positive쪽에 치우침
 
plot(lda.fit) #up이 중심으로 좀 더 와있는 모습
 
lda.pred=predict(lda.fit, Smarket.2005)
names(lda.pred) #class는 분류해놓은 결과, oisterior값은 임계치값
lda.class=lda.pred$class
table(lda.class,Direction.2005)
 
mean(lda.class==Direction.2005) #정분류율 56%
 
sum(lda.pred$posterior[,1]>=.5)
 
sum(lda.pred$posterior[,1]<.5)
 
lda.pred$posterior[1:20,1] #up, down class가 logistic이랑 반대인 상황(지금은 down을 추정하는 상황임)
 
lda.class[1:20]
 
sum(lda.pred$posterior[,1]>.9)
 
 
################################################
 
# Quadratic Discriminant Analysis
 
qda.fit=qda(Direction~Lag1+Lag2,data=Smarket,subset=train) #LDA와 QDA의 차이 잘 알고 할 것
qda.fit #group means가 약간달라짐을 확인가능
 
qda.class=predict(qda.fit,Smarket.2005)$class
table(qda.class,Direction.2005)
 
mean(qda.class==Direction.2005) #예측값이 60%정도로 LDA와 Logistic보단 향상된 모습을 보임
 
################################################
 
# K-Nearest Neighbors
 
library(class)
train.X=cbind(Lag1,Lag2)[train,]
test.X=cbind(Lag1,Lag2)[!train,]
train.Direction=Direction[train]
set.seed(1)
knn.pred=knn(train.X,test.X,train.Direction,k=3)
#1번째 인수에 훈련자료, 2번째 자료에는 테스트자료, 세번째 자료에는 훈련자료에서의 response y값, 4번째 인수에는 k값
table(knn.pred,Direction.2005)
 
mean(knn.pred==Direction.2005)

* 참고링크 : https://rpubs.com/evertonjlima/242623

RPubs

RPubs - ISLR Ch4 Solutions