[ISL] 6장 - 예측변수 선택(Stepwise, CV)(R 실습)

* 이론 : 업로드 예정

* 소스코드 원본 : http://faculty.marshall.usc.edu/gareth-james/ISL

 

1. 기초통계량 분석 및 결측치 처리

#install.packages("ISLR")  library(ISLR) #fix(Hitters) names(Hitters) dim(Hitters) sum(is.na(Hitters$Salary)) Hitters=na.omit(Hitters) dim(Hitters) ters=na.omit(Hitters) dim(Hitters)

2. Best Subset Choice

#install.packages("leaps") library(leaps) #regsubsets() : best subset choice가 가능한 함수 regfit.full=regsubsets(Salary~.,Hitters)  summary(regfit.full)

- 특정한 설정을 하지 않으면 최대 8개의 best subsets 까지 가능하다.

- 별표가 많이 표시된 변수가 최적의 변수인데, 연봉에 영향을 미치는 최적의 예측변수는 CRBI 변수이다.(즉, CRBI 변수가 포함되면 좋다.)

- 단, 7~8개짜리 예측변수를 고려하게 되면 CRBI 변수는 빠진다.(즉, 다른 변수의 조합이 더 좋다.)

regfit.full=regsubsets(Salary~.,data=Hitters,nvmax=19) #예측변수를 8개 이상 갖고 싶을 땐, nvmax로 설정 reg.summary=summary(regfit.full) names(reg.summary) reg.summary$rsq

- 1~19개까지의 예측변수를 고려하였을 때의 결정 계수 값인데, 변수가 많아질수록 점점 커지므로 rsq로 예측변수를 선택해선 안된다. (이 때, 사용하는 것이 BIC, AIC 등이 있다.)

 

3. RSS, Adj R-sq, Cp, BIC로 적당한 예측변수의 개수를 찾아보기

par(mfrow=c(2,2)) plot(reg.summary$rss, xlab="Number of Variables", ylab="RSS", type="l") plot(reg.summary$adjr2, xlab="Number of Variables", ylab="Adjusted RSq", type="l") which.max(reg.summary$adjr2) points(11, reg.summary$adjr2[11], col="red",cex=2,pch=20) plot(reg.summary$cp, xlab="Number of Variables", ylab="Cp",type='l') which.min(reg.summary$cp) points(10, reg.summary$cp[10], col="red", cex=2, pch=20) which.min(reg.summary$bic) plot(reg.summary$bic, xlab="Number of Variables", ylab="BIC", type='l') points(6, reg.summary$bic[6], col="red", cex=2, pch=20)

- 1번 : rss값
- 2번 : adj rsq(11정도에서 제일 큼) 
- 3번 : cp(10정도)
- 4번 : bic(6정도, 제일 단순)

par(mfrow=c(2,2)) plot(regfit.full,scale="r2") plot(regfit.full,scale="adjr2") #adj R-sq일 때, 모두 다 들어간건 0.51(값이 제일 큰 모형은 11개의 예측변수가 포함됨) plot(regfit.full,scale="Cp")  plot(regfit.full,scale="bic") #bic는 6개가 들어간 경우 coef(regfit.full,6) #최종 선택 모형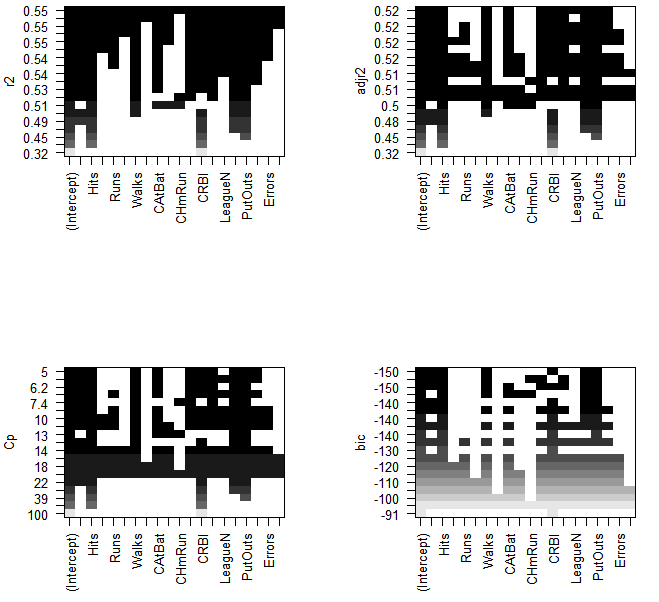

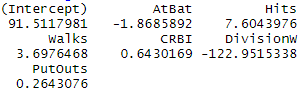
- 최종적으로 6개의 예측변수 선택

 

4. Forward stepwise

regfit.fwd=regsubsets(Salary~.,data=Hitters,nvmax=19,method="forward") summary(regfit.fwd)

하단 생략

5. Backward Stepwise

regfit.bwd=regsubsets(Salary~.,data=Hitters,nvmax=19,method="backward") summary(regfit.bwd)

6. 비교

coef(regfit.full,7) coef(regfit.fwd,7) coef(regfit.bwd,7)

- 예측변수를 모두 7개로 설정하였을 때, Forward Stepwise의 성능이 제일 좋다.

- 예측변수로써는 Atbat, Hits 등이 있다.(위의 결과 확인)

 

7. CV로 예측변수 선택하기

#CV로 선택하는 하는 경우 set.seed(1) #T or F가 hitters의 크기만큼 담긴 바구니 안에서 복원추출 실시 train=sample(c(TRUE,FALSE), nrow(Hitters),rep=TRUE) test=(!train)#train과 반대되는 data를 test set으로 설정 regfit.best=regsubsets(Salary~.,data=Hitters[train,],nvmax=19) test.mat=model.matrix(Salary~.,data=Hitters[test,]) val.errors=rep(NA,19) for(i in 1:19){   coefi=coef(regfit.best,id=i)   pred=test.mat[,names(coefi)]%*%coefi   val.errors[i]=mean((Hitters$Salary[test]-pred)^2) } val.errors #10일 때 min이 되는 것을 확인 가능 which.min(val.errors) #언제 min이 되냐 라는 뜻 coef(regfit.best,7) #min일 때 coef 값

 

- 예측변수가 7개 일 때, val.errors가 최소

- 예측변수는 Atbat, Hits 등 7개

 

8. K-fold로 선택하기(K=10일 때)

#10-fold하는 과정 k=10 set.seed(1) folds=sample(1:k,nrow(Hitters),replace=TRUE) cv.errors=matrix(NA,k,19, dimnames=list(NULL, paste(1:19))) for(j in 1:k){   best.fit=regsubsets(Salary~.,data=Hitters[folds!=j,],nvmax=19)   for(i in 1:19){     pred=predict(best.fit,Hitters[folds==j,],id=i)     cv.errors[j,i]=mean( (Hitters$Salary[folds==j]-pred)^2)   } } mean.cv.errors=apply(cv.errors,2,mean) which.min(mean.cv.errors)

- 10개 일 때, error 값이 가장 낮음

par(mfrow=c(1,1)) plot(mean.cv.errors,type='b') reg.best=regsubsets(Salary~.,data=Hitters, nvmax=19) coef(reg.best,11)