[ISL] 6장 - 연습문제 (R 실습)

※ 6장의 연습문제 중 8번, 9번, 11번만 진행하였습니다.

 

문제 원본 : http://faculty.marshall.usc.edu/gareth-james/ISL/ISLR%20Seventh%20Printing.pdf

 * 위 교재 256페이지

 

문제

==========================================================================

8(a). rnorm()을 사용하여 predictor vector와 noise vector를 만드시오.(n=100)

8(b). n=100인 vector Y를 만드시오. 여기서 베타값은 랜덤으로 선택하시오.

8(c). 예측 변수 X, X2, ..., X10이 포함된 최상의 모형을 선택하려면 최상의 부분 집합을 선택하십시오. 이 때, Cp, BIC, adj R-sq에 따라 적합한 모델을 선택하시오.

8(d). stepwise seletion을 이용하여 8(c)를 다시 구하시오.

8(e). CV를 사용하여 적절한 lambda를 찾아 lasso model을 적합시키시오.

==========================================================================

9(a). "College" data set을 training set과 test set으로 나누시오.

9(b). Training set에 최소 제곱법을 사용하여 선형 모델을 적합시키시오.

9(c). Training set에 Ridge Regression을 적합시키시오.

9(d). Training set에 Lasso Regression을 적합시키시오.

==========================================================================

11(a). "Boston" data set을 활용하여 subset selection으로 적절하게 적합할 예측변수의 개수를 찾으시오. 

11(b). the lasso를 활용하여 Boston data set을 적합시키시오.

11(c). ridge regression을 활용하여 (b)를 다시 구하시오.

==========================================================================

 

해답

8(a)

set.seed(1) n=100 x=rnorm(n) #Predictor vector  e=rnorm(n) #noise vector

8(b)

betas=sample(1:n,4) y=betas[1]+betas[2]*x+betas[3]*x^2+betas[4]*x^3+e

8(c)

library(leaps) PrintBestModelByScore=function(model,score,ord=which.min){   model.summary=summary(model)   model.bestcoef=ord(model.summary[[score]])   model.which=model.summary$which[model.bestcoef,]      print(coef(model,model.bestcoef)) } y.bestsub=regsubsets(y~poly(x,10,raw = T),data=data.frame(x,y),method = 'exhaustive') PrintBestModelByScore(y.bestsub,'cp') PrintBestModelByScore(y.bestsub,'bic') PrintBestModelByScore(y.bestsub,'adjr2',ord=which.max)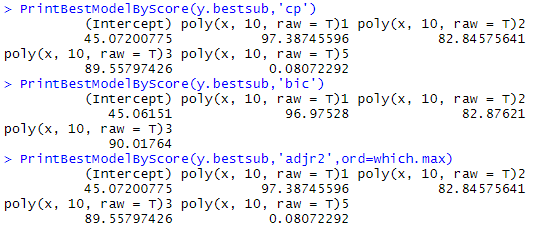

par(mfrow=c(2,2)) # plots for(score in c('cp','bic','adjr2','rsq'))    plot(x=summary(y.bestsub)[[score]],xlab='Number of Predictors',ylab=score,type='l')

 

 

- 3개를 선택했을 때가 가장 좋아보인다.

 

8(d)

# Forward selection y.forward=regsubsets(y~poly(x,10,raw = T),data=data.frame(x,y),method = 'forward') PrintBestModelByScore(y.forward,'cp') PrintBestModelByScore(y.forward,'bic') PrintBestModelByScore(y.forward,'adjr2',ord=which.max) # plots par(mfrow=c(2,2)) for(score in c('cp','bic','adjr2','rsq'))    plot(x=summary(y.forward)[[score]],xlab='Number of Predictors',ylab=score,type='l')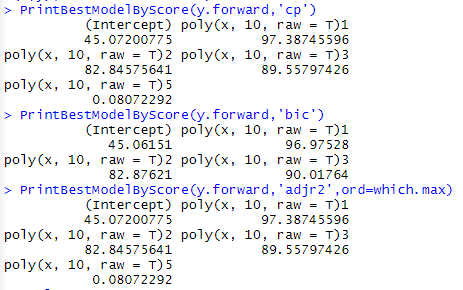

- Forward stepwise 역시 3개의 예측변수를 선택했을 때 가장 좋아보였다.

 

# Barckward Selection y.backward=regsubsets(y~poly(x,10,raw=T),data=data.frame(x,y),method = 'backward') PrintBestModelByScore(y.backward,'cp') PrintBestModelByScore(y.backward,'bic') PrintBestModelByScore(y.backward,'adjr2',ord=which.max) # plots par(mfrow=c(2,2)) for(score in c('cp','bic','adjr2','rsq'))    plot(x=summary(y.backward)[[score]],xlab='Number of Predictors',ylab=score,type='l')

- Backward Stepwise 또한 3개의 예측변수를 선택했을 때 성능이 가장 좋다.

 

8(e)

library(glmnet) y.lasso.cv = cv.glmnet(poly(x,degree = 10,raw = T),y) y.lasso.cv$lambda.min #7.968629 y.lasso.cv$lambda.1se par(mfrow=c(1,1)) plot(data.frame(y.lasso.cv$lambda, y.lasso.cv$cvm),xlab='Lambda',ylab='Mean Cross Validation Error',type='l')

- lambda값 = 7.968629

predict(y.lasso.cv, s=y.lasso.cv$lambda.min, type = "coefficients")

- 3개의 예측변수를 두었을 때 가장 성능이 좋음

y.lasso.pred = predict(y.lasso.cv, s=y.lasso.cv$lambda.min, newx = poly(x,10,raw=T)) curve(betas[1]+betas[2]*x+betas[3]*x^2,from=-3, to=3, xlab="x", ylab="y") points(data.frame(x,y),col='red') points(data.frame(x,y.lasso.pred),col='blue')

- 모델의 예측이 관찰된 데이터를 거의 따르고 있다.(즉, 모델의 성능이 좋다.)

 

==========================================================================

 

9(a)

data("College") set.seed(1) trainid <- sample(1:nrow(College), nrow(College)/2) train <- College[trainid,] test <- College[-trainid,] str(College)

9(b)

fit.lm <- lm(Apps~., data=train) pred.lm <- predict(fit.lm, test) (err.lm <- mean((test$Apps - pred.lm)^2))  # test error, 1135758

9(c)

xmat.train <- model.matrix(Apps~., data=train)[,-1] xmat.test <- model.matrix(Apps~., data=test)[,-1] fit.ridge <- cv.glmnet(xmat.train, train$Apps, alpha=0) (lambda <- fit.ridge$lambda.min)  # optimal lambda, 405.8404 pred.ridge <- predict(fit.ridge, s=lambda, newx=xmat.test) (err.ridge <- mean((test$Apps - pred.ridge)^2))  # test error, 976261.5

9(d)

xmat.train <- model.matrix(Apps~., data=train)[,-1]  xmat.test <- model.matrix(Apps~., data=test)[,-1]  fit.ridge <- cv.glmnet(xmat.train, train$Apps, alpha=1)  (lambda <- fit.ridge$lambda.min)  # optimal lambda, 1.97344 pred.ridge <- predict(fit.ridge, s=lambda, newx=xmat.test)  (err.ridge <- mean((test$Apps - pred.ridge)^2))  # test error, 1115901

- 릿지 Regression의 성능이 가장 우수하다.

 

==========================================================================

 

11(a)

# split data into training and test sets set.seed(2) trainid <- sample(1:nrow(Boston), nrow(Boston)/2) train <- Boston[trainid,] test <- Boston[-trainid,] xmat.train <- model.matrix(crim~., data=train)[,-1] xmat.test <- model.matrix(crim~., data=test)[,-1] #forward stwpwise fit.fwd = regsubsets(crim~., data=train, nvmax = ncol(Boston)-1) fwd.summary = summary(fit.fwd) fwd.summary err.fwd <- rep(NA, ncol(Boston)-1) for(i in 1:(ncol(Boston)-1)) {   pred.fwd <- predict(fit.fwd, test, id=i)   err.fwd[i] <- mean((test$crim - pred.fwd)^2) } plot(err.fwd, type="b", main="Test MSE for Forward Selection", xlab="Number of Predictors") which.min(err.fwd)

- 변수가 4개 일 때, 가장 성능이 좋음

#backward stepwise fit.back = regsubsets(crim~., data=train, nvmax = ncol(Boston)-1) back.summary = summary(fit.back) back.summary err.back <- rep(NA, ncol(Boston)-1) for(i in 1:(ncol(Boston)-1)) {   pred.back <- predict(fit.back, test, id=i)   err.back[i] <- mean((test$crim - pred.back)^2) } plot(err.back, type="b", main="Test MSE for backward Selection", xlab="Number of Predictors") which.min(err.back)

- 변수 4개 일 때, 성능이 가장 좋다

par(mfrow=c(3,2)) min.cp <- which.min(fwd.summary$cp)   plot(fwd.summary$cp, xlab="Number of Poly(X)", ylab="Forward Selection Cp", type="l") points(min.cp, fwd.summary$cp[min.cp], col="red", pch=4, lwd=5) min.cp <- which.min(back.summary$cp)   plot(back.summary$cp, xlab="Number of Poly(X)", ylab="Backward Selection Cp", type="l") points(min.cp, back.summary$cp[min.cp], col="red", pch=4, lwd=5) min.bic <- which.min(fwd.summary$bic)   plot(fwd.summary$bic, xlab="Number of Poly(X)", ylab="Forward Selection BIC", type="l") points(min.bic, fwd.summary$bic[min.bic], col="red", pch=4, lwd=5) min.bic <- which.min(back.summary$bic)   plot(back.summary$bic, xlab="Number of Poly(X)", ylab="Backward Selection BIC", type="l") points(min.bic, back.summary$bic[min.bic], col="red", pch=4, lwd=5) min.adjr2 <- which.max(fwd.summary$adjr2)   plot(fwd.summary$adjr2, xlab="Number of Poly(X)", ylab="Forward Selection Adjusted R^2", type="l") points(min.adjr2, fwd.summary$adjr2[min.adjr2], col="red", pch=4, lwd=5) min.adjr2 <- which.max(back.summary$adjr2)   plot(back.summary$adjr2, xlab="Number of Poly(X)", ylab="Backward Selection Adjusted R^2", type="l") points(min.adjr2, back.summary$adjr2[min.adjr2], col="red", pch=4, lwd=5)

 

11(b)

# ridge regression model fit.ridge <- cv.glmnet(xmat.train, train$crim, alpha=0) (lambda <- fit.ridge$lambda.min)  # optimal lambda, 0.5675919 pred.ridge <- predict(fit.ridge, s=lambda, newx=xmat.test) (err.ridge <- mean((test$crim - pred.ridge)^2))  # test error, 20.50985

11(c)

# the lasso fit.lasso <- cv.glmnet(xmat.train, train$crim, alpha=1) (lambda <- fit.lasso$lambda.min)  # optimal lambda, 0.0652597 pred.lasso <- predict(fit.lasso, s=lambda, newx=xmat.test) (err.lasso <- mean((test$crim - pred.lasso)^2))  # test error, 20.50298

- 비슷하지만 Lasso의 결과가 미세하게 더 좋다.