[ISL] 7장 - 비선형모델(Local regression, Smoothing splines, GAM) 이해하기(R 실습)

* 이론 : 업로드 예정

* 소스코드 원본 : http://faculty.marshall.usc.edu/gareth-james/ISL

 

※ 사용 데이터 : Wage

1. 바로 4차 다항식 적합시켜보기

library(ISLR) attach(Wage) fit=lm(wage~poly(age,4),data=Wage) coef(summary(fit)) fit2=lm(wage~poly(age,4,raw=T),data=Wage) coef(summary(fit2))

- 4차 다항식의 P-value가 0.05인 것으로 보아 유의미한 것을 알 수 있음

agelims=range(age) #age의 min과 max를 찍는다. age.grid=seq(from=agelims[1],to=agelims[2]) preds=predict(fit,newdata=list(age=age.grid),se=TRUE) #se도 함께 계산하겠다.(band를 같이 그리고 싶으면 se=True, 아니면 false) se.bands=cbind(preds$fit+ 2*preds$se.fit, preds$fit-2*preds$se.fit) par(mfrow=c(1,1),mar=c(4.5,4.5,1,1),oma=c(0,0,4,0)) plot(age,wage,xlim=agelims,cex=.5,col="darkgrey") title("Degree-4 Polynomial",outer=T) lines(age.grid,preds$fit,lwd=2,col="blue") #plot 위에 라인 그리는거 matlines(age.grid,se.bands,lwd=1,col="blue",lty=3)#라인을 여러 개 그리겠다.

1-2. 바로 4차 다항식을 적합시키는 것이 정당할까?(다른 n차 다항식의 결과도 확인해보는 과정)

fit.1=lm(wage~age,data=Wage) #1차 fit.2=lm(wage~poly(age,2),data=Wage) #2차(2차항의 계수가 0이면 1차가 되는 것) fit.3=lm(wage~poly(age,3),data=Wage) #3차 fit.4=lm(wage~poly(age,4),data=Wage) #4차 fit.5=lm(wage~poly(age,5),data=Wage) #5차(즉, 차수가 점점 커지는건 점점 모형이 커지고 있다는 것) anova(fit.1,fit.2,fit.3,fit.4,fit.5) #통계적으로 유의성을 띄는지 검사할 때 하는 아노바 검사

- Pvalue를 보면 추가된 cof가 0인지를 검사할 수 있다.
- Pvalue가 0.05보다 작거나 같은 2,3,4번째 항을 추가했을 때, 결과가 좋음을 알 수 있다.

fit.1=lm(wage~education+age,data=Wage) #education 변수 추가 fit.2=lm(wage~education+poly(age,2),data=Wage) #fit2는 edu는 그대로 두고 2차식 적합 fit.3=lm(wage~education+poly(age,3),data=Wage) #fit3는 edu는 그대로 두고 3차식 적합 fit.4=lm(wage~education+poly(age,4),data=Wage) anova(fit.1,fit.2,fit.3,fit.4)

- 결과를 보면 edu를 포함시키지 않았을 때와 결과가 다르므로 변수를 포함시켰을 때 n차식을 고려해야함
- 3차식까지 유의미한 결과를 볼 수 있음

 

1-3. 나이에 따른 고소득 수준 판단(wage>250이면 고소득으로 정하였음)

fit=glm(I(wage>250)~poly(age,4),data=Wage,family=binomial) preds=predict(fit,newdata=list(age=age.grid),se=T) pfit=exp(preds$fit)/(1+exp(preds$fit)) se.bands.logit = cbind(preds$fit+2*preds$se.fit, preds$fit-2*preds$se.fit) se.bands = exp(se.bands.logit)/(1+exp(se.bands.logit)) preds=predict(fit,newdata=list(age=age.grid),type="response",se=T) plot(age,I(wage>250),xlim=agelims,type="n",ylim=c(0,.2)) points(jitter(age), I((wage>250)/5),cex=.5,pch="|",col="darkgrey") lines(age.grid,pfit,lwd=2, col="blue") matlines(age.grid,se.bands,lwd=1,col="blue",lty=3)

- 30대 초반 이후 고소득이 증가하는 모습을 보이다 60대 중반부터 급격히 하락하는 모습이 보인다.

 

2. Regression Splines

library(splines) fit=lm(wage~bs(age,knots=c(25,40,60)),data=Wage)  # default : cubic  #knots를 25,40,60 3개로 자른 상황 pred=predict(fit,newdata=list(age=age.grid),se=T) plot(age,wage,col="gray") lines(age.grid,pred$fit,lwd=2) lines(age.grid,pred$fit+2*pred$se,lty="dashed") lines(age.grid,pred$fit-2*pred$se,lty="dashed")

2-1. 적절한 knots를 찾는 방법

> attr(bs(age,df=6),"knots") #찾아진 나트 값 25%   50%   75%  33.75 42.00 51.00

- 위에서 나트를 지정했는데, bs를 할 때 나트를 지정하지 않고 bs개수로 지정이 가능
- uniform quantile basis가 나트를 자동으로 잡아줌
- 특별한 일이 아니면 uniform quantile basis으로 나트를 잡는게 안전하다.

 

2-2. nature spline 적합

fit2=lm(wage~ns(age,df=4),data=Wage) pred2=predict(fit2,newdata=list(age=age.grid),se=T) lines(age.grid, pred2$fit,col="red",lwd=2)

- bs와 비슷한 수준이다.

 

2-3. CV로 적합

plot(age,wage,xlim=agelims,cex=.5,col="darkgrey") title("Smoothing Spline") fit=smooth.spline(age,wage,df=16) fit2=smooth.spline(age,wage,cv=TRUE)   fit2$df   lines(fit,col="red",lwd=2) lines(fit2,col="blue",lwd=2) legend("topright",legend=c("16 DF","6.8 DF"),col=c("red","blue"),lty=1,lwd=2,cex=.8

- CV를 적합시켰을 때, 결과가 비슷하지만 자유도가 더 낮다.

 

3. Local Regression

plot(age,wage,xlim=agelims,cex=.5,col="darkgrey") title("Local Regression") fit=loess(wage~age,span=.2,data=Wage) fit2=loess(wage~age,span=.5,data=Wage) lines(age.grid,predict(fit,data.frame(age=age.grid)),col="red",lwd=2) lines(age.grid,predict(fit2,data.frame(age=age.grid)),col="blue",lwd=2) legend("topright",legend=c("Span=0.2","Span=0.5"),col=c("red","blue"),lty=1,lwd=2,cex=.8)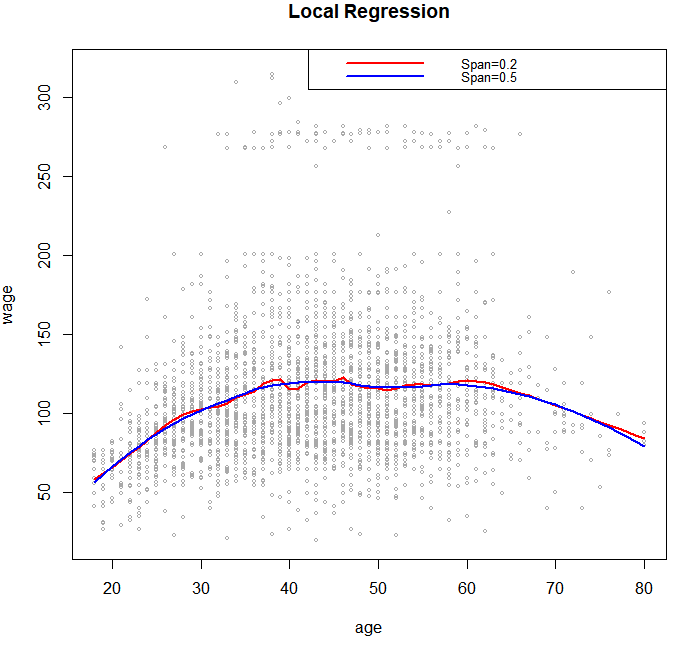

- 결과를 보면 span을 작게하면 민감하게 따라갈 수 있음
- 단, smooth하지 않은 추정치를 줄 수 있음
- span이 크면 민감하게 따라가진 못하지만 smooth한 추정치를 줄 수 있음
- 즉, 적절한 span을 주는 것도 중요하다.

 

4. GAMs

library(ISLR) library(splines) gam1=lm(wage~ns(year,4)+ns(age,5)+education,data=Wage) # gam with natural splines  #gam은 non-linear가 불가해서 마지막에 education을 추가해 주어야함 library(gam)   gam.m3=gam(wage~s(year,4)+s(age,5)+education,data=Wage) # gam with smoothing splines (df = 4 or 5) #gam1은 neture spline, gam.m3는 spline #자유도가 커지면 찌글찌글(복잡), 작으면 단순   par(mfrow=c(1,3)) plot(gam.m3, se=TRUE,col="blue") plot.Gam(gam1, se=TRUE, col="red")

- 반응변수에 주는 영향이 비선형인지 선형인지 모를 때, 함수 형태의 가정을 하지 않고 모양을 보고 선형으로 해도 괜찮은지 판단을 해야함
- 나이가 같고 edu가 같으면 임금이 올라가다가 한번 떨어지는 구간이 있음
- age는 선형이라고 보기 어렵다
- year는 커브를 보았을 때는 애매하며, conf_band를 보았을 때 true curve를 추정한 상태임.
- 따라서, linear function을 비슷하게 그려보았을 때, band 안에 포함되도록 그릴 수 없으므로 linear로 불가함

 

gam.m1=gam(wage~s(age,5)+education,data=Wage) #non-linear하게  gam.m2=gam(wage~year+s(age,5)+education,data=Wage) #year에 s를 안붙힌건 age를 linear하게 적합시키겠다.(즉, m1에서 m3로 갈수록 복잡한 모형) anova(gam.m1,gam.m2,gam.m3,test="F")   # H0 linear vs H1: not H0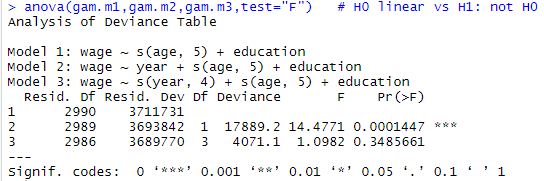

- m2는 대립가설이 채택되므로 유의미하다. 즉, year를 선형이다라는 대립가설은 유의미하다.

 

summary(gam.m3)

- s(year, 4)의 pvalue는 0인지 아닌지
- s(age, 5)의 pvalue는 나이에 따라 linear로 변한다.