[ISL] 7장 - 연습문제 (R 실습)

※ 1장의 연습문제 중 6번, 9번, 10번만 진행하였습니다.

 

문제 원본 : http://faculty.marshall.usc.edu/gareth-james/ISL/ISLR%20Seventh%20Printing.pdf

 * 위 교재 279페이지

 

문제

==========================================================================

6(a). Wage의 age를 사용하여 Polynimial Regression을 적합시키시오. 단, CV를 활용하여 적절한 차수를 구하고 ANOVA를 통해 해당 차수가 적절한지 보이시오
6(b). Wage의 age를 사용하여 Step Function을 적합시키시오. 또한 Cut의 개수는 CV를 활용하여 선택하시오.

==========================================================================

9. Boston Data set의 dis 변수를 예측변수로, nox를 반응변수로 두어 다음을 해결하시오.

9(c). 적절한 Polynomial의 차수를 구하고 결과를 설명하시오.

9(f). 최적의 자유도를 찾아 regression spline을 적합하시오.

==========================================================================

10. College data set을 활용하여 다음을 해결하시오.

10(a). training과 test set을 나눈 후, forward stepwise selection과 backward stepwise selection으로 예측변수를 선택하시오.

10(b). GAM을 training set에 적합시키시오.

10(c). test set을 model에 적합시켜 평가하고, 그에 대한 결과를 설명하시오.

10(d). 어떤 변수가 비선형 관계와 반응한다는 증거가 있는지 설명하시오.

==========================================================================

 

해답

6(a)

library(ISLR) library(boot) data(Wage) set.seed(1) cv.error = rep(0,10) for (i in 1:10){   glm.fit = glm(wage~poly(age,i), data=Wage)   cv.error[i] = cv.glm(Wage, glm.fit, K=10)$delta[1] } cv.error which.min(cv.error) plot(cv.error, type='b')

# ANOVA fit.01 <- lm(wage~age, data=Wage) fit.02 <- lm(wage~poly(age,2), data=Wage) fit.03 <- lm(wage~poly(age,3), data=Wage) fit.04 <- lm(wage~poly(age,4), data=Wage) fit.05 <- lm(wage~poly(age,5), data=Wage) fit.06 <- lm(wage~poly(age,6), data=Wage) fit.07 <- lm(wage~poly(age,7), data=Wage) fit.08 <- lm(wage~poly(age,8), data=Wage) fit.09 <- lm(wage~poly(age,9), data=Wage) fit.10 <- lm(wage~poly(age,10), data=Wage) anova(fit.01,fit.02,fit.03,fit.04,fit.05,fit.06,fit.07,fit.08,fit.09,fit.10)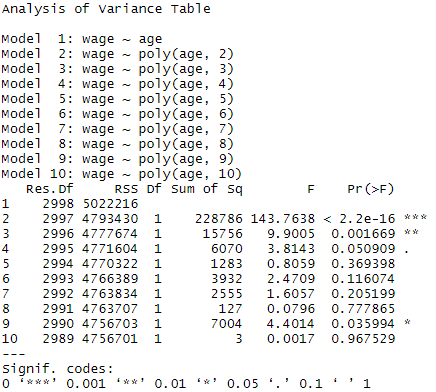

- 4차 일 때, P-value가 0.05에 가까워 유의미함을 알 수 있다.

- 따라서, 차수를 4로 결정

agelims = range(Wage$age) age.grid = seq(agelims[1], agelims[2]) preds = predict(fit.04, newdata = list(age=age.grid), se=TRUE) se.bands = preds$fit + cbind(2*preds$se.fit, -2*preds$se.fit) par(mfrow=c(1,1), mar=c(4.5,4.5,1,1), oma=c(0,0,4,0)) plot(Wage$age, Wage$wage, xlim=agelims, cex=0.5, col="darkgrey") title("Degree 4 Polynomial Fit", outer=TRUE) lines(age.grid, preds$fit, lwd=2, col="blue") matlines(age.grid, se.bands, lwd=1, col="blue", lty=3)

 

6(b)

set.seed(1) # cross-validation cv.error <- rep(0,9) for (i in 2:10) {   Wage$age.cut <- cut(Wage$age,i)   glm.fit <- glm(wage~age.cut, data=Wage)   cv.error[i-1] <- cv.glm(Wage, glm.fit, K=10)$delta[1]  # [1]:std, [2]:bias-corrected } cv.error plot(2:10, cv.error, type="b")

 

- cut의 개수는 8이 적당해보인다. 

# going with 8 cuts cut.fit <- glm(wage~cut(age,8), data=Wage) preds <- predict(cut.fit, newdata=list(age=age.grid), se=TRUE) se.bands <- preds$fit + cbind(2*preds$se.fit, -2*preds$se.fit) plot(Wage$age, Wage$wage, xlim=agelims, cex=0.5, col="darkgrey") title("Fit with 8 Age Bands") lines(age.grid, preds$fit, lwd=2, col="blue") matlines(age.grid, se.bands, lwd=1, col="blue", lty=3)

 

==========================================================================

 

9(c)

data(Boston) set.seed(1) cv.error=rep(0,10) for (i in 1:10){   glm.fit = glm(nox~poly(dis,i), data = Boston)   cv.error[i] = cv.glm(Boston, glm.fit, K=10)$delta[1] } cv.error which.min(cv.error) #4 plot(cv.error, type="b")  fit.04 = lm(nox~poly(dis,4), data=Boston) dislims = range(Boston$dis) dis.grid = seq(dislims[1], dislims[2]) preds = predict(fit.04, newdata = list(dis=dis.grid), se=TRUE) se.bands = preds$fit + cbind(2*preds$se.fit, -2*preds$se.fit) par(mfrow=c(1,1), mar=c(4.5,4.5,1,1), oma=c(0,0,4,0)) plot(Boston$dis, Boston$nox, xlim=dislims, cex=0.5, col="darkgrey") title("Degree 4 Polynomial Fit") lines(dis.grid, preds$fit, lwd=2, col="blue") matlines(dis.grid, se.bands, lwd=1, col="blue", lty=3) summary(fit.04)

 

- 3차가 더 적절해보임

 

9(f)

data(Boston) set.seed(1) cv.error <- rep(0,7) for (i in 4:10) {   glm.fit <- glm(nox~bs(dis, df=i), data=Boston)   cv.error[i-3] <- cv.glm(Boston, glm.fit, K=10)$delta[1] } cv.error plot(4:10, cv.error, type="b")  # df=5로 결정 attr(bs(Boston$dis,df=5),"knots") #찾아진 나트 값 dis.grid=seq(from=range(Boston$dis)[1],to=range(Boston$dis)[2]) plot(Boston$dis,Boston$nox,col="gray") fit = lm(nox~bs(dis, df=5, knots = 2.384033, 4.325700),data = Boston) pred = predict(fit, newdata = list(dis=dis.grid),se=T) lines(dis.grid, pred$fit,col="blue",lwd=2) fit2=lm(nox~ns(dis,df=5),data=Boston) pred2=predict(fit2,newdata=list(dis=dis.grid),se=T) lines(dis.grid, pred2$fit,col="red",lwd=2)

- NS가 조금 더 부드러운 모습을 보인다.

 

==========================================================================

 

10(a)

library(ISLR) library(leaps) data(College) set.seed(1) trained = sample(1:nrow(College), nrow(College)/2) train = College[trained,] test = College[-trained,] head(College) fit.fwd = regsubsets(Outstate ~., data=train, nvmax=ncol(College)-1) fwd.summary = summary(fit.fwd) fwd.summary

err.fwd <- rep(NA, ncol(College)-1) for(i in 1:(ncol(College)-1)) {   pred.fwd <- predict(fit.fwd, test, id=i)   err.fwd[i] <- mean((test$Outstate - pred.fwd)^2) } par(mfrow=c(2,2)) plot(err.fwd, type="b", main="Test MSE", xlab="Number of Predictors") min.mse <- which.min(err.fwd)   points(min.mse, err.fwd[min.mse], col="red", pch=4, lwd=5) plot(fwd.summary$adjr2, type="b", main="Adjusted R^2", xlab="Number of Predictors") max.adjr2 <- which.max(fwd.summary$adjr2)   points(max.adjr2, fwd.summary$adjr2[max.adjr2], col="red", pch=4, lwd=5) plot(fwd.summary$cp, type="b", main="cp", xlab="Number of Predictors") min.cp <- which.min(fwd.summary$cp)   points(min.cp, fwd.summary$cp[min.cp], col="red", pch=4, lwd=5) plot(fwd.summary$bic, type="b", main="bic", xlab="Number of Predictors") min.bic <- which.min(fwd.summary$bic)   points(min.bic, fwd.summary$bic[min.bic], col="red", pch=4, lwd=5)

- BIC를 통해 6개의 예측변수가 적절하다고 판단

 

10(b)

gam.fit <- gam(Outstate ~                   Private +   # categorical variable                  s(Room.Board,3) +                   s(Terminal,3) +                   s(perc.alumni,3) +                   s(Expend,3) +                   s(Grad.Rate,3),                 data=College) par(mfrow=c(2,3)) plot(gam.fit, se=TRUE, col="blue")

10(c)

pred <- predict(gam.fit, test) (mse.error <- mean((test$Outstate - pred)^2)) #3718850 err.fwd[which.min(err.fwd)] #4083998

- GAM이 더 우수한 성능을 보인다.

 

10(d)

- Expend에 대한 비선형 효과의 강력한 증거가 보인다.